All-in-One PicoCTF Writeups: Crypto

S1l3ntC0nquer2024-11-262024-12-19

Preface

In fact, there seems to be nothing to say about the preface, but I just don’t want to classify the topics at the beginning, so I still put a preface XD.

When I was brushing PicoCTF, I often found that almost all writeups were in English, so I wanted to write a more complete Gujarati version! In short, I will try my best to collect all the picoCTF questions here (but because I have already written about 60 questions before I start to write writeup, I may wait for the other parts to be completed before filling in the previous part), if necessary You can just come here to see all the writeups, that’s it! Hope this helps.

My scripts & note on Github
[Cryptography Notebook : The Meridian of Cryptography](https://s1l3ntc0nquer.github.io/web/StudyNotes/Cryptography-Notes-: The Meridian of Cryptography/)

Easy1

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
   +----------------------------------------------------
A | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
B | B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
C | C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
D | D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
E | E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
F | F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
G | G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
H | H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
I | I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
J | J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
K | K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
L | L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
M | M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
N | N O P Q R S T U V W X Y Z A B C D E F G H I J K L M
O | O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
P | P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
Q | Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
R | R S T U V W X Y Z A B C D E F G H I J K L M N O P Q
S | S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
T | T U V W X Y Z A B C D E F G H I J K L M N O P Q R S
U | U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
V | V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
W | W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
X | X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Y | Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
Z | Z A B C D E F G H I J K L M N O P Q R S T U V W X Y

Cipher: UFJKXQZQUNB
Key: SOLVECRYPTO

This question is a Vigenère cipher. The Vigenère cipher (French: Chiffre de Vigenère, also translated as the Vigenère cipher) is an encryption algorithm that uses a series of Caesar ciphers to form a cipher alphabet. It is a single form of polyalphabetic ciphers. [Wikipedia](https://zh.wikipedia.org/zh-tw/Virginia Code)
The decryption method is also very simple. The top column is the plain text, and the leftmost row is the KEY. In this way, the corresponding characters in the middle are the cipher text. After knowing this, you can push it back to get the clear text.

cipher = "UFJKXQZQUNB"
key = "SOLVECRYPTO"

pt = ""

for i in range(len(cipher)):
    shift = ord(key[i]) - 65  # Get the offset of the key letter
    c = ord(cipher[i])  # Get the current letter in the ciphertext

    c = (c - shift - 65) % 26 + 65  # Decrypt using offset
    pt += chr(c)

print(f"Message: {pt}")

And the final flag is as follows

picoCTF{CRYPTOISFUN}

Caesar

As the title says, this question is a basic Caesar encryption. The question gives an encrypted flag

picoCTF{gvswwmrkxlivyfmgsrhnrisegl}

Just use the string inside to decrypt it. Because you don’t know what the offset is, you use brute force to crack it.

cipher = "gvswwmrkxlivyfmgsrhnrisegl"


def caesar_cipher(text, shift):
    plaintext = ""
    for c in text:
        plaintext += chr((ord(c) - 97 + shift) % 26 + 97)
    return plaintext


for i in range(26):
    plaintext = caesar_cipher(cipher, i)
    print(f"Shift {i}: {plaintext}")

Among the results, it seems that crossingtherubicondjneoach is the most reasonable, so this is the flag.

picoCTF{crossingtherubicondjneoach}

New Caesar

The question gives a ciphertext and a Python script.

apbopjbobpnjpjnmnnnmnlnbamnpnononpnaaaamnlnkapndnkncamnpapncnbannaapncndnlnpna

import string

LOWERCASE_OFFSET = ord("a")
ALPHABET = string.ascii_lowercase[:16]

def b16_encode(plain):
	enc = ""
	for c in plain:
		binary = "{0:08b}".format(ord(c))
		enc += ALPHABET[int(binary[:4], 2)]
		enc += ALPHABET[int(binary[4:], 2)]
	return enc

def shift(c, k):
	t1 = ord(c) - LOWERCASE_OFFSET
	t2 = ord(k) - LOWERCASE_OFFSET
	return ALPHABET[(t1 + t2) % len(ALPHABET)]

flag = "redacted"
key = "redacted"
assert all([k in ALPHABET for k in key])
assert len(key) == 1

b16 = b16_encode(flag)
enc = ""
for i, c in enumerate(b16):
	enc += shift(c, key[i % len(key)])
print(enc)

First observe this encryption script. It was found that after converting the Ascii value of each letter of the plaintext into Binary, he added 0s from the left to 8 Bits, and then divided each 4-bit block into one block. The binary digits (0 ~ 15) of each block were mapped to Base16 characters. Set (a ~ p). Then use this thing to make a shift, which is a transformation of Caesar encryption.

In short, the decryption is done in reverse, so I won’t explain it in detail. The exploit is as follows:

import string

LOWERCASE_OFFSET = ord("a")
ALPHABET = string.ascii_lowercase[:16]


def b16_encode(plain):
    enc = ""
    for c in plain:
        binary = "{0:08b}".format(ord(c))
        enc += ALPHABET[int(binary[:4], 2)]  # Since 4 bits can represent 16 characters
        enc += ALPHABET[int(binary[4:], 2)]
    return enc


def b16_decode(b16):
    dec = ""
    for c in range(0, len(b16), 2):
        first = b16[c]
        second = b16[c + 1]
        first_index = ALPHABET.index(first)
        second_index = ALPHABET.index(second)
        binary = bin(first_index)[2:].zfill(4) + bin(second_index)[2:].zfill(4)
        dec += chr(int(binary, 2))
    return dec


def shift(c, k):
    t1 = ord(c) - LOWERCASE_OFFSET  # (c - 97 + k - 97) % 16 = result
    t2 = ord(k) - LOWERCASE_OFFSET
    return ALPHABET[(t1 + t2) % len(ALPHABET)]  # two numbers sum modulo 16


def inverse_shift(c, k):
    t1 = ord(c) - LOWERCASE_OFFSET
    t2 = ord(k) - LOWERCASE_OFFSET
    return ALPHABET[(t1 - t2) % len(ALPHABET)]  # two numbers difference modulo 16


enc = "apbopjbobpnjpjnmnnnmnlnbamnpnononpnaaaamnlnkapndnkncamnpapncnbannaapncndnlnpna"
for key in ALPHABET:
    dec = ""
    for i, c in enumerate(enc):
        dec += inverse_shift(c, key[i % len(key)])
    b16_dec = b16_decode(dec)
    print(f"Decrypted flag: {b16_dec}")

After brute force cracking, the one that looks most like Flag is et_tu?_23217b54456fb10e908b5e87c6e89156. Finally, I wrapped it myself with picoCTF{} and submitted it, and it turned out to be correct.

picoCTF{et_tu?_23217b54456fb10e908b5e87c6e89156}

rotation

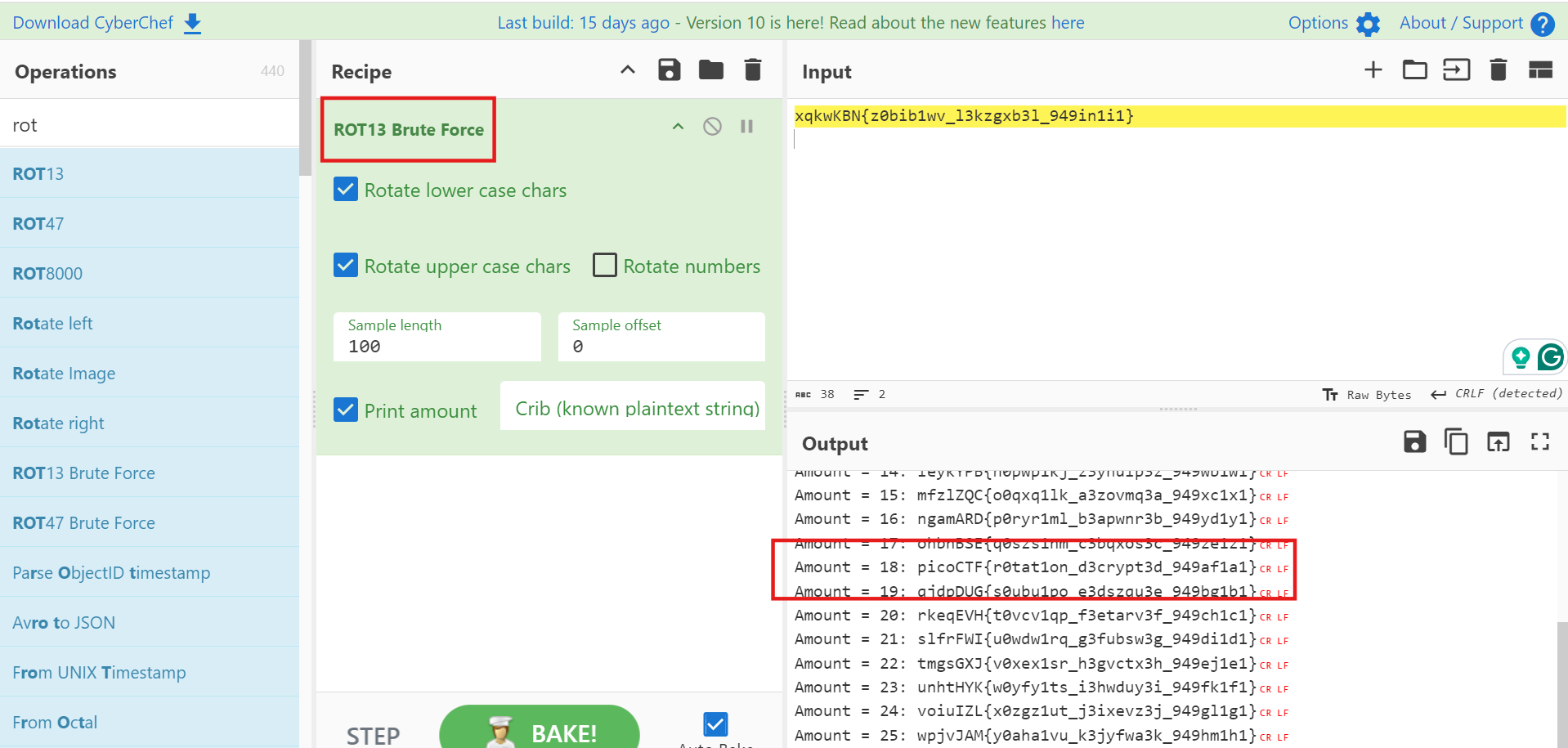
This question gives an encrypted ciphertext.

xqkwKBN{z0bib1wv_l3kzgxb3l_949in1i1}

It seems to be Transposition Cipher, directly used to crack the Caesar cipher on the Internet. CyberChef is used here.

picoCTF{r0tat1on_d3crypt3d_949af1a1}

Mind your Ps and Qs

This question is about RSA encryption. Let’s first review the process and parameters in RSA encryption.

$\text{Find two prime numbers } p \text{ and } q$
$n = p \times q$
$\phi(n) = (p-1) \times (q-1)$
$e \text{ is the encryption exponent}$
$d = e^{-1} \mod \phi(n)$
$c \text{ is the encrypted message}; \quad c = m^e \mod n$
$m \text{ is the message}; \quad m = c^d \mod n$
$\text{Public key} = (e, n)$
$\text{Private key} = (d, n)$

After reviewing, look at the description of the question.

Description:
In RSA, a small e value can be problematic, but what about N? Can you decrypt this?
==============================
Decrypt my super sick RSA:
c: 421345306292040663864066688931456845278496274597031632020995583473619804626233684
n: 631371953793368771804570727896887140714495090919073481680274581226742748040342637
e: 65537

The description of this question tells us that when e is too small, we can use a low public key exponential attack (Low public exponent attack), and the question asks us to think about how we can use it when N is too small.

After going back and looking at the RSA encryption process, we found that N is the product of two prime numbers, and when N is too small, we can brute force crack out two P and Q. Here we directly use FactorDB to find the factors of N, and then we can find P and Q.

With P and Q, we can follow the RSA process to find the plaintext M. I wrote a Python to help me find the plaintext, as follows

from Crypto.Util.number import inverse, long_to_bytes
from factordb.factordb import FactorDB


def long2str(long_int: int) -> str:
    return long_to_bytes(long_int).decode()


c = 421345306292040663864066688931456845278496274597031632020995583473619804626233684
n = 631371953793368771804570727896887140714495090919073481680274581226742748040342637
e = 65537

# From Factor db find p and q
f = FactorDB(n)
f.connect()
factors = f.get_factor_list()
p = factors[0]
q = factors[1]

phi_n = (p - 1) * (q - 1)

d = inverse(e, phi_n)
print(f"Private key: d = {d}")
m = pow(c, d, n)
print(f"Decrypted message: m = {long2str(m)}")

The plaintext found in the end will be a large number. At this time, use long_to_bytes of Crypto.Util.number and decode it to convert it into a string, and you can get the flag.

picoCTF{sma11_N_n0_g0od_55304594}

No padding, no problem

You can read this article first Day 14:[Discrete Mathematics] What is Congruence (Mod)?

When we decrypt the ciphertext given in the question, he will say Will not decrypt the ciphertext. Try Again. The program representing the question should be detecting whether the input we entered is Ciphertext. and we know

$Plaintext = c^d \mod n$

$c^d \mod n = (c+n)^d \mod n$

So after we add the c and n given in the question, and input it into his program, we will get:

Here you go: 290275030195850039473456618367455885069965748851278076756743720446703314517401359267322769037469251445384426639837648598397

Then just use Crypto’s long_to_bytes3 method to find the plaintext, as follows:

from Crypto.Util.number import long_to_bytes
from pwn import *

r = remote("mercury.picoctf.net", 10333)
r.recvuntil("n:")
n = int(r.recvline().strip())
r.recvuntil("ciphertext:")
c = int(r.recvline().strip())
num = n + c
r.sendline(str(num))
r.recvuntil("Here you go:")
m = int(r.recvline().strip())
r.close()

print(long_to_bytes(m))

picoCTF{m4yb3_Th0se_m3s54g3s_4r3_difurrent_1772735}

interencdec

The question gives the ciphertext enc_flag, as follows.

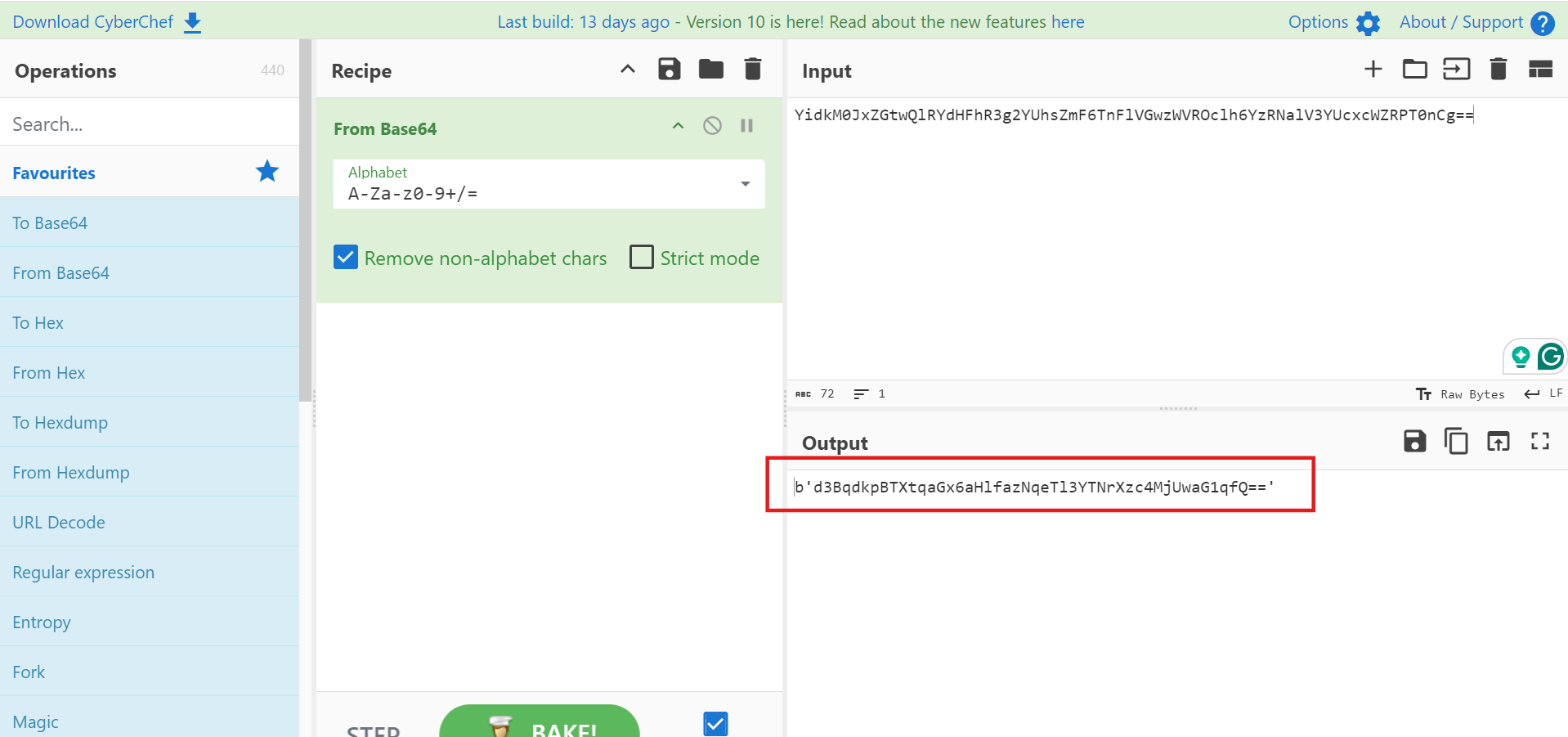
YidkM0JxZGtwQlRYdHFhR3g2YUhsZmF6TnFlVGwzWVROclh6YzRNalV3YUcxcWZRPT0nCg==

Because the last two == make it look like a base64 format, so use base64 to decode it first. The tool used here is CyberChef, which can perform many types of encoding, decoding, encryption, etc. online.

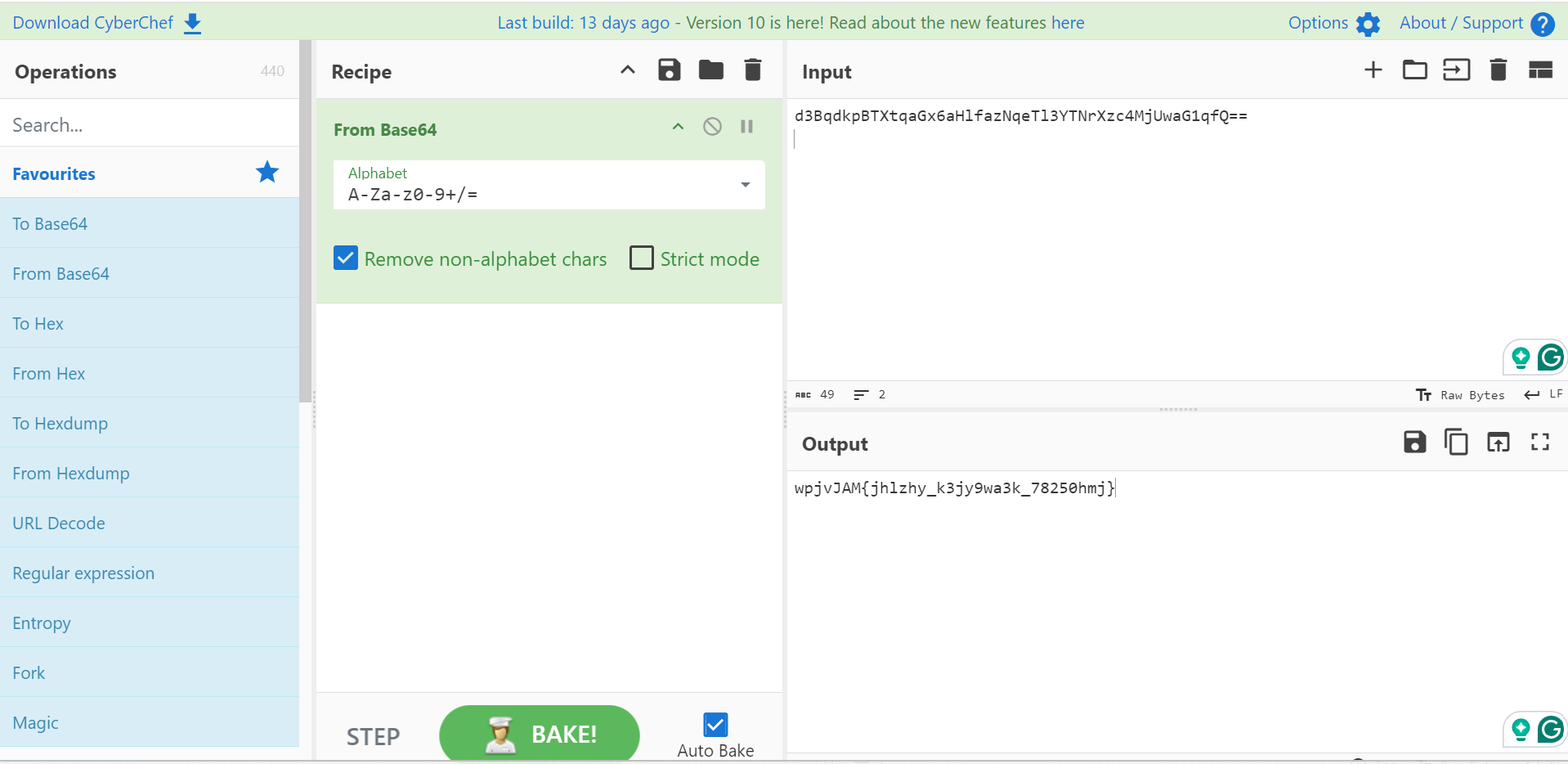
d3BqdkpBTXtqaGx6aHlfazNqeTl3YTNrXzc4MjUwaG1qfQ==

After decoding once, it looked like this, still very similar to the base64 format, so I did base64 decoding again. (Note: The preceding b should be removed here, leaving only the content in quotation marks)

wpjvJAM{jhlzhy_k3jy9wa3k_78250hmj}

After decoding it again, it changed into this shape. It seems that there is already a prototype of Flag (because of the curly brackets), so I guess it is some kind of substitution cipher. Just use the most common Caesar cipher to solve it violently! The exploit is as follows:

enc_flag = input("Enter the encrypted flag: ")

for i in range(1, 27):
    dec_flag = ""
    for char in enc_flag:
        if char.isalpha():
            if char.isupper():
                dec_flag += chr((ord(char) - ord("A") - i) % 26 + ord("A"))
            else:
                dec_flag += chr((ord(char) - ord("a") - i) % 26 + ord("a"))
        else:
            dec_flag += char
    if "pico" in dec_flag.lower():
        print(dec_flag)

picoCTF{caesar_d3cr9pt3d_78250afc}

Easy peasy

If you want to know about OTP, you can check out this [One-Time Pad](https://zh.wikipedia.org/zh-tw/One-Time Pad)

Let’s look at the title first.

******************Welcome to our OTP implementation!******************
This is the encrypted flag!
551e6c4c5e55644b56566d1b5100153d4004026a4b52066b4a5556383d4b0007

What data would you like to encrypt?

In this question, we have to first read the Code he gave us. In the encrypt function we can see a few things. Because the length of the Cipher given in the question is 64, and because it outputs the Cipher in hexadecimal, we can know that the length of the key_location he used is 32, that is to say, when we encrypt next time It is the key starting from the 33rd bit.

def encrypt(key_location):
    ui = input("What data would you like to encrypt? ").rstrip()
    if len(ui) == 0 or len(ui) > KEY_LEN:
        return -1

    start = key_location  #Start from 32 here
    stop = key_location + len(ui)

    kf = open(KEY_FILE, "rb").read()

    if stop >= KEY_LEN:
        stop = stop % KEY_LEN
        key = kf[start:] + kf[:stop]
    else:
        key = kf[start:stop]
    key_location = stop

    result = list(map(lambda p, k: "{:02x}".format(ord(p) ^ k), ui, key))

    print("Here ya go!\n{}\n".format("".join(result)))

    return key_location

After knowing that the first time we input the inscription to be encrypted is from the 32nd key, we need to find a way to use the same set of keys as in the question, and we can find something in this section of the code.

if stop >= KEY_LEN:
        stop = stop % KEY_LEN
        key = kf[start:] + kf[:stop]

Here, if we make stop and KEY_LEN equal, so stop % KEY_LEN == 0, stop will be set to 0, so we can make the one-time pad reused Got it! So we first enter a bunch of useless characters to fill that interval, let it end the first 50000 loop, and after entering the loop again, we can get the same key as the title.

And because his encryption method is to calculate XOR, we can simply calculate the XOR again to get the plaintext, as follows:

key \oplus pt = ct$$ $$key \oplus ct = pt$$ $$pt \oplus ct = key

from pwn import *
import binascii  # binascii.unhexlify() is used to convert hex to binary

offset = 50000 - 32

r = remote("mercury.picoctf.net", 11188)

print(r.recvline())
print(r.recvline())
encrypted_flag = r.recvline().strip()

print(encrypted_flag)

r.recvuntil(b"?")
r.sendline(b"A" * offset)
r.recvuntil(b"?")
r.sendline(b"A" * 32)
r.recvline()

encoded = r.recvline().strip()
encoded = binascii.unhexlify(encoded)

message = "A" * 32
key = []
for i in range(len(encoded)):
    key.append(ord(message[i]) ^ encoded[i])

flag = []
encrypted_flag = binascii.unhexlify(encrypted_flag)
for i in range(len(encrypted_flag)):
    flag.append(chr(key[i] ^ encrypted_flag[i]))

flag = "".join(flag)
print(flag)

Custom encryption

This question is given to two files. One is the encrypted flag, which also contains some variables required for encryption; the other is the encryption script. Now that the script is given, let’s take a look at the Code first. I combined the encrypted flag information given in the question and wrote the annotations directly into the code. Take a look!

from random import randint
import sys


def generator(g, x, p):
    return pow(g, x) % p


# Cipher text = ASCII code of each character of plain text * key * 311 and append to a list
def encrypt(plaintext, key):
    cipher = []
    for char in plaintext:
        cipher.append(((ord(char) * key * 311)))
    return cipher


def is_prime(p):
    v = 0
    for i in range(2, p + 1):
        if p % i == 0:
            v = v + 1
    if v > 1:
        return False
    else:
        return True


def dynamic_xor_encrypt(plaintext, text_key):
    cipher_text = ""
    key_length = len(text_key)
    for i, char in enumerate(plaintext[::-1]):  #Start from the end of plaintext
        key_char = text_key[i % key_length]  # Loop through each character in text_key
        encrypted_char = chr(ord(char) ^ ord(key_char))  # Corresponding ciphertext = plaintext ^ key
        cipher_text += encrypted_char
    return cipher_text


def test(plain_text, text_key):
    p = 97
    g = 31
    if not is_prime(p) and not is_prime(g):
        print("Enter prime numbers")
        return
    a = randint(p - 10, p)
    b = randint(g - 10, g)
    print(f"a = {a}")
    print(f"b = {b}")

    # a = 89
    # b = 27
    # p = 97
    # g = 31
    u = generator(g, a, p)  # u = 31 ** 89 % 97 = 49
    v = generator(g, b, p)  # u = 31** 27 % 97 = 85
    key = generator(v, a, p)  # key = 85 ** 89 % 97 = 12
    b_key = generator(u, b, p)  # b_key = 49 ** 27 % 97 = 12
    shared_key = None
    if key == b_key:
        shared_key = key  # shared_key = 12
    else:
        print("Invalid key")
        return
    semi_cipher = dynamic_xor_encrypt(plain_text, text_key)
    cipher = encrypt(semi_cipher, shared_key)
    print(f"cipher is: {cipher}")


if __name__ == "__main__":
    message = sys.argv[1]
    test(message, "trudeau")

From the above code, we can know that it has been encrypted twice. The first time is to reverse the plaintext and let it do XOR on the text_key loop. The second time is to convert the first encryption to ASCII and multiply it. key is then multiplied by 311.

For decryption, do the opposite, first divide it by 311 and then divide it by the key (here 12) to get a semi-ciphertext (semi_cipher). Next, the semi-ciphertext needs to be reversed first, and then the function written in it is used to perform The plaintext needs to be reversed again to get the correct flag. As for why it needs to be reversed twice, the explanation is as follows:

Assume that the dynamic_xor_encrypt of the question is f and the plaintext is ABC.

encryption:
f(ABC, KEY) = C'B'A'

Decryption:
The first reversal changes C'B'A into A'B'C, so the XOR of C'B'A to KEY will be calculated in f
f(A'B'C, KEY) = CBA
The second reversal, convert CBA to ABC
flag=ABC

Hope this explanation is a little clearer! In short, you can get the flag by decrypting it like this. The following is the code for My decryption:

def decrypt(cipher: list, key: int, text_key: str) -> str:
    semi_cipher = ""
    for encrypted_value in cipher:
        decrypted_value = encrypted_value // (key * 311)  # Use // Return
        semi_cipher += chr(decrypted_value)
    semi_cipher = semi_cipher[::-1]  # Reverse the ciphertext
    plaintext = dynamic_xor_encrypt(semi_cipher, text_key)
    return plaintext


cipher = [
    33588,
    276168,
    261240,
    302292,
    343344,
    328416,
    242580,
    85836,
    82104,
    156744,
    0,
    309756,
    78372,
    18660,
    253776,
    0,
    82104,
    320952,
    3732,
    231384,
    89568,
    100764,
    22392,
    22392,
    63444,
    22392,
    97032,
    190332,
    119424,
    182868,
    97032,
    26124,
    44784,
    63444,
]
plaintext = decrypt(cipher, 12, "trudeau")  # since we know the key is 12
print(f"plaintext is: {plaintext[::-1]}")

picoCTF{custom_d2cr0pt6d_dc499538}

Mini RSA

The question gives a set of RSA encrypted ciphertext and the public key (n, e), as follows.

N: 1615765684321463054078226051959887884233678317734892901740763321135213636796075462401950274602405095138589898087428337758445013281488966866073355710771864671726991918706558071231266976427184673800225254531695928541272546385146495736420261815693810544589811104967829354461491178200126099661909654163542661541699404839644035177445092988952614918424317082380174383819025585076206641993479326576180793544321194357018916215113009742654408597083724508169216182008449693917227497813165444372201517541788989925461711067825681947947471001390843774746442699739386923285801022685451221261010798837646928092277556198145662924691803032880040492762442561497760689933601781401617086600593482127465655390841361154025890679757514060456103104199255917164678161972735858939464790960448345988941481499050248673128656508055285037090026439683847266536283160142071643015434813473463469733112182328678706702116054036618277506997666534567846763938692335069955755244438415377933440029498378955355877502743215305768814857864433151287
e: 3

ciphertext (c): 1220012318588871886132524757898884422174534558055593713309088304910273991073554732659977133980685370899257850121970812405700793710546674062154237544840177616746805668666317481140872605653768484867292138139949076102907399831998827567645230986345455915692863094364797526497302082734955903755050638155202890599808147130204332030239454609548193370732857240300019596815816006860639254992255194738107991811397196500685989396810773222940007523267032630601449381770324467476670441511297695830038371195786166055669921467988355155696963689199852044947912413082022187178952733134865103084455914904057821890898745653261258346107276390058792338949223415878232277034434046142510780902482500716765933896331360282637705554071922268580430157241598567522324772752885039646885713317810775113741411461898837845999905524246804112266440620557624165618470709586812253893125417659761396612984740891016230905299327084673080946823376058367658665796414168107502482827882764000030048859751949099453053128663379477059252309685864790106

It is not difficult to find that the public key index e of this question is very small, only 3. So we use Coppersmith’s attack, Low public exponent attack. Since the question says that $m^e$ is slightly larger than $n$ , the solution principle is as follows ( $c$ is the ciphertext, $m$ is the plaintext, $e$ is the public key index, $n$ is the public key module number):

$c=m^e\mod n$

$m^e=k\times n+c$

$\text{Bruteforce k and find the eth root of }k\times n+c$

To calculate the plaintext, I wrote a Python script as follows.

import gmpy2
from Crypto.Util.number import long_to_bytes

# Declare n, e, c given by the question
n = 1615765684321463054078226051959887884233678317734892901740763321135213636796075462401950274602405095138589898087428337758445013281488966866073355710771864671726991918706558071231266976427184673800225254531695928541272546385146495736420261815693810544589811104967829354461491178200126099661909654163542661541699404839644035177445092988952614918424317082380174383819025585076206641993479326576180793544321194357018916215113009742654408597083724508169216182008449693917227497813165444372201517541788989925461711067825681947947471001390843774746442699739386923285801022685451221261010798837646928092277556198145662924691803032880040492762442561497760689933601781401617086600593482127465655390841361154025890679757514060456103104199255917164678161972735858939464790960448345988941481499050248673128656508055285037090026439683847266536283160142071643015434813473463469733112182328678706702116054036618277506997666534567846763938692335069955755244438415377933440029498378955355877502743215305768814857864433151287
e = 3
c = 1220012318588871886132524757898884422174534558055593713309088304910273991073554732659977133980685370899257850121970812405700793710546674062154237544840177616746805668666317481140872605653768484867292138139949076102907399831998827567645230986345455915692863094364797526497302082734955903755050638155202890599808147130204332030239454609548193370732857240300019596815816006860639254992255194738107991811397196500685989396810773222940007523267032630601449381770324467476670441511297695830038371195786166055669921467988355155696963689199852044947912413082022187178952733134865103084455914904057821890898745653261258346107276390058792338949223415878232277034434046142510780902482500716765933896331360282637705554071922268580430157241598567522324772752885039646885713317810775113741411461898837845999905524246804112266440620557624165618470709586812253893125417659761396612984740891016230905299327084673080946823376058367658665796414168107502482827882764000030048859751949099453053128663379477059252309685864790106

# Brute force k * n + c's e-th root
k = 0
while True:
    m, is_root = gmpy2.iroot(k * n + c, e)
    if is_root:
        break
    else:
        k += 1

# Convert numbers to strings
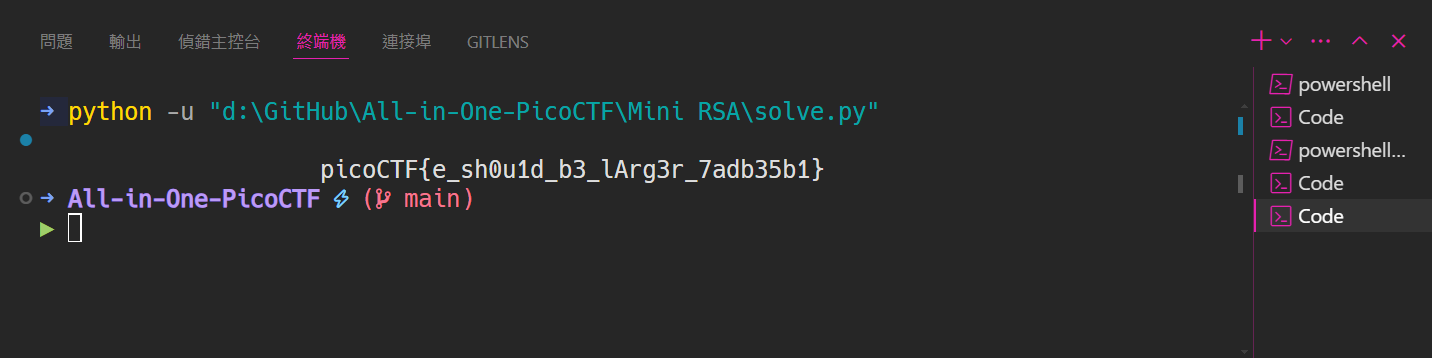
print(long_to_bytes(m).decode())

After execution, you can find the flag~

picoCTF{e_sh0u1d_b3_lArg3r_7adb35b1}

miniRSA

The principle of this question is exactly the same as the above question, both are that e is too small, so a small public key index attack is used. If you want to know more detailed principles, please see [the question above](http://localhost:4000/CTF/All-in-One PicoCTF-Writeups/#Mini-RSA). Go directly to Exploit here.

import gmpy2
from Crypto.Util.number import long_to_bytes

# Declare n, e, c given by the question
n = 29331922499794985782735976045591164936683059380558950386560160105740343201513369939006307531165922708949619162698623675349030430859547825708994708321803705309459438099340427770580064400911431856656901982789948285309956111848686906152664473350940486507451771223435835260168971210087470894448460745593956840586530527915802541450092946574694809584880896601317519794442862977471129319781313161842056501715040555964011899589002863730868679527184420789010551475067862907739054966183120621407246398518098981106431219207697870293412176440482900183550467375190239898455201170831410460483829448603477361305838743852756938687673
e = 3
c = 2205316413931134031074603746928247799030155221252519872650080519263755075355825243327515211479747536697517688468095325517209911688684309894900992899707504087647575997847717180766377832435022794675332132906451858990782325436498952049751141
# Brute force k * n + c's e-th root
k = 0
while True:
    m, is_root = gmpy2.iroot(k * n + c, e)
    if is_root:
        break
    else:
        k += 1

# Convert numbers to strings
print(long_to_bytes(m).decode())

picoCTF{n33d_a_lArg3r_e_d0cd6eae}

b00tl3gRSA2

This question gives a Netcat connection method nc jupiter.challenges.picoctf.org 57464. Let’s connect to the host first and take a look. After connecting in, you can get the public key (e, n) and ciphertext C.

c: 34445152657892770965998909208982810010756495888304322276986171688963957553047312382212965383503534206383273951160130679579064667281298014647933151624988393675732505770685953145935008017740630822545491396331269103186466894080672218590474311310524848042116230603776754439341606635542489964403857509012413327600
n: 68119657260892882095325897664190568273401102037961904922092525598421583896728037063388427153386051029888075348478917163527609699475528597669779479757588723783858410926089233944915463760773669961431608182207070211704104302242228666666950454789023679482670607533342993172566630254264627616929496230133089420521
e: 37080866881034431981182406871995949206609767233841813908107646836499839869322256469420054910921271502986970536597423895034064361029486896285600240175045808110268909882526287214985406985265436522819284777174250321264328876332147142628536767687999620602780344780826878645902905435208326564999474536627301460973

In the description of the topic he said:

In RSA d is a lot bigger than e, why don’t we use d to encrypt instead of e?

This means that in this question he interchanged $d$ and $e$ and used $d$ to encrypt $e$ . The following article explains in detail why this approach should not be used.

[RSA: Does it matter if you use e or d to encrypt?](https://crypto.stackexchange.com/questions/54557/rsa-does-it-matter-if-you-use-e-or- d-to-encrypt)

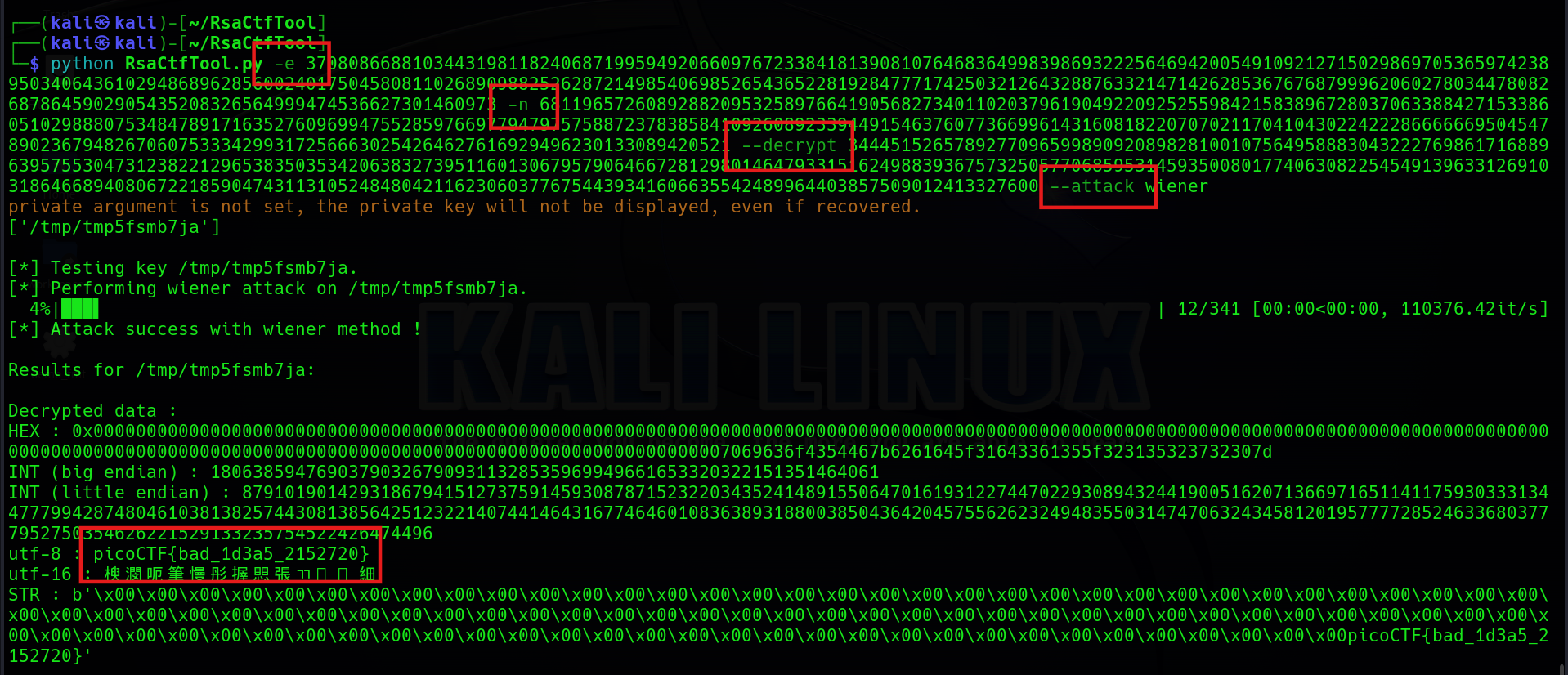
ૐIn short, when the private key index ( $d$ ) is relatively small, Wiener’s attack can be used. An open source tool can be used here to help us quickly execute the attack.

RsaCtfTool

Please check the official documentation for usage. In short, the exploit is as follows.

python RsaCtfTool.py -e 37080866881034431981182406871995949206609767233841813908107646836499839869322256469420054910921271502986970536597423895034064361029486896285600240175045808110268909882526287214985406985265436522819284777174250321264328876332147142628536767687999620602780344780826878645902905435208326564999474536627301460973 -n 68119657260892882095325897664190568273401102037961904922092525598421583896728037063388427153386051029888075348478917163527609699475528597669779479757588723783858410926089233944915463760773669961431608182207070211704104302242228666666950454789023679482670607533342993172566630254264627616929496230133089420521 --decrypt 34445152657892770965998909208982810010756495888304322276986171688963957553047312382212965383503534206383273951160130679579064667281298014647933151624988393675732505770685953145935008017740630822545491396331269103186466894080672218590474311310524848042116230603776754439341606635542489964403857509012413327600 --attack wiener

In short, after setting all the parameters, you can successfully get the Flag.

picoCTF{bad_1d3a5_2152720}

b00tl3gRSA3

This question is the same as the previous question. First use Netcat to connect to the host and get the following information.

c: 1155433454658603081887942538070618568058048531029758454280998255793925425541835159695263849863790503010031220771999047690488595295467625987010931696477313386062384452816188902386984531395080585643524053777943484599038478398898775019494628236550977835910935567524611329303821647514235510296512723444159728500460371101677191814101634547011569775
n: 3009815969095519381043948515174929441467634594821498333858615496361783804562611599728570248270874306617036697889577813844217713194056663725350522605669349001546826005570895246471872723077264759401472551915667965016802426155245585986786567513487278588996436597960321248870612409759311004096684257474660765774013406405351078796165091907796029759
e: 65537

The title said

Why use p and q when I can use more?

This means that the initial primes in this problem are not just $p$ and $q$ . So we only need to find the Euler function $\phi(n)$ and follow the normal process. Since it does not only have two prime numbers $p$ and $q$ , it will be much easier to decompose. The exploit is as follows.

from sympy.ntheory import factorint
from Crypto.Util.number import long_to_bytes


def get_phi(n):
    f = factorint(n) # Return a dictionary, the key is the prime factor, and the value is the power of the prime factor
    phi = 1
    for a, b in f.items():
        phi *= pow(a, b - 1) * (a - 1)
    return phi


# Announce the information given by the question
c = 1155433454658603081887942538070618568058048531029758454280998255793925425541835159695263849863790503010031220771999047690488595295467625987010931696477313386062384452816188902386984531395080585643524053777943484599038478398898775019494628236550977835910935567524611329303821647514235510296512723444159728500460371101677191814101634547011569775
n = 3009815969095519381043948515174929441467634594821498333858615496361783804562611599728570248270874306617036697889577813844217713194056663725350522605669349001546826005570895246471872723077264759401472551915667965016802426155245585986786567513487278588996436597960321248870612409759311004096684257474660765774013406405351078796165091907796029759
e = 65537

phi = get_phi(n)
d = pow(e, -1, phi)
m = pow(c, d, n)

print(long_to_bytes(m))

Here get_phi(n) uses the following formula for finding the Euler function：

$\phi(n) = p_1^{k_1 - 1} \times (p_1 - 1) \times p_2^{k_2 - 1} \times (p_2 - 1) \times \cdots \times p_m^{k_m - 1} \times (p_m - 1)$

After calculating $\phi(n)$ in this way, you can use the normal calculation process to find the plaintext $m$ .

picoCTF{too_many_fact0rs_8606199}

Vigenere

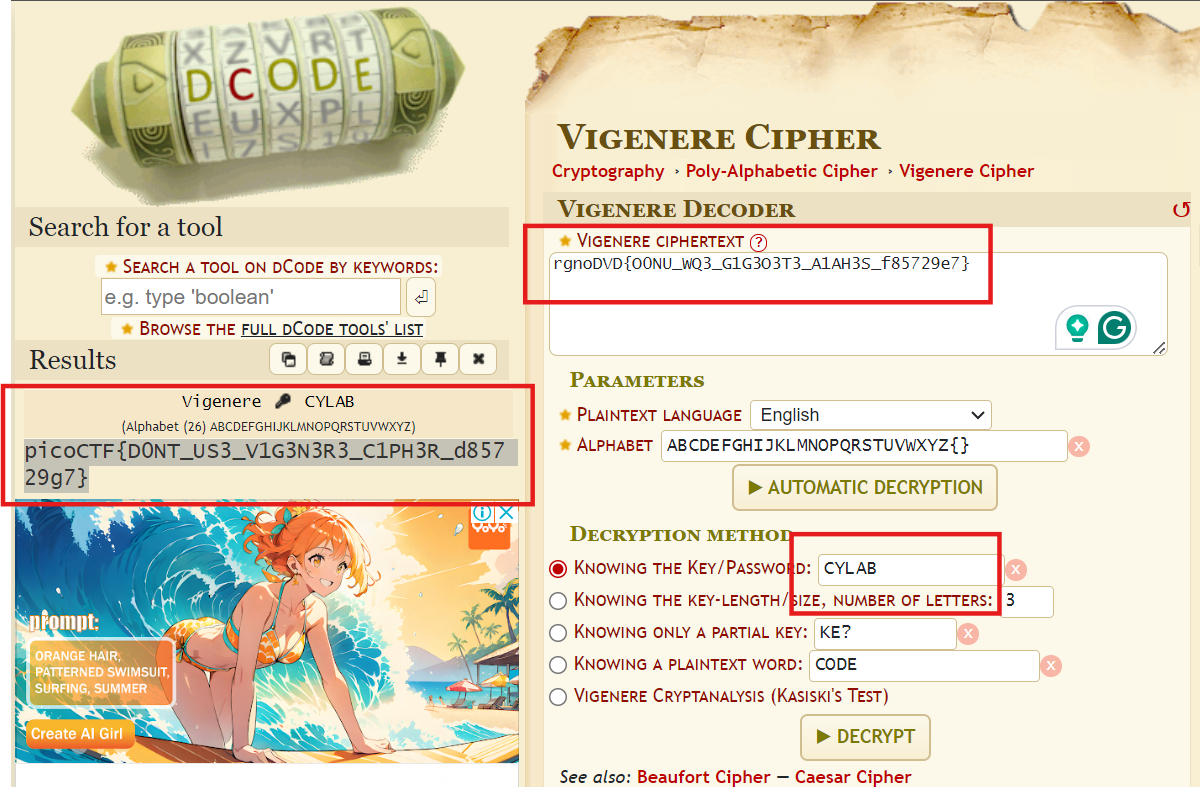
This question gives an encrypted ciphertext and Key, and the question also tells us that it is a Vigenere Cipher. We can just use the Online decoder to solve it. (I don’t know why its difficulty is Medium LMAO)

picoCTF{D0NT_US3_V1G3N3R3_C1PH3R_d85729g7}

Pixelated

This question gives two pictures, and it is something called Visual Cryptography. The title picture is as follows。

Here I use Stegsolve to combine two images. First open the first image, click Analyze > Image Combiner, and then click the second image. After that, it will pop up an interface for you to choose the Combine method. The default is XOR. Keep clicking the right arrow until the method changes to ADD and you can see the Flag.

picoCTF{d562333d}

After I finished solving it, I looked at other people’s Writeups, and I found that someone solved it using Python and thought it was cool, so I attached it for everyone to see. (Writeup)

# import Image
from PIL import Image

# open both photos
i1 = Image.open('scrambled1.png')
i2 = Image.open('scrambled2.png')

# get width and height
width1, height1 = i1.size

# open new image
i3 = Image.new('RGB', (width1, height1))

# load the pixels
pixels = i3.load()

# loop through all pixels
for i in range(width1):
    for j in range(height1):
        # xor the values
        x = i1.getpixel((i,j))[0] ^ i2.getpixel((i,j))[0]
        y = i1.getpixel((i,j))[1] ^ i2.getpixel((i,j))[1]
        z = i1.getpixel((i,j))[2] ^ i2.getpixel((i,j))[2]

        # if all white then convert to black
        if (x,y,z) == (255,255,255):
            (x,y,z) = (0,0,0)

        # put the new pixels in place
        i3.putpixel((i,j), (x,y,z))

# save the image
i3.save("test.png", "PNG")

HideToSee

This question gave a picture, and the words written on the picture said that it was an Atbash Cipher. After checking, it was a Substitution Cipher with the order of letters reversed. The Tips say to Extract it, so I guess you need to use Steghide. Here, extract the Data first.

steghide extract -sf atbash.jpg

This will extract an encrypted.txt file and take a look at the contents.

krxlXGU{zgyzhs_xizxp_8z0uvwwx}

Just take this to online decryption tool, and the Flag will come out.

picoCTF{atbash_crack_8a0feddc}

college-rowing-team

This question gives an encryption script and a ciphertext (including public key). Let’s take a look at the encryption script encrypt.py first.

#!/usr/bin/env python3

import random
from Crypto.Util.number import getPrime, bytes_to_long


with open("flag.txt", "rb") as f:
    flag = f.read()

msgs = [
    b"I just cannot wait for rowing practice today!",
    b"I hope we win that big rowing match next week!",
    b"Rowing is such a fun sport!",
]

msgs.append(flag)
msgs *= 3
random.shuffle(msgs)

for msg in msgs:
    p = getPrime(1024)
    q = getPrime(1024)
    n = p * q
    e = 3
    m = bytes_to_long(msg)
    c = pow(m, e, n)
    with open("encrypted-messages.txt", "a") as f:
        f.write(f"n: {n}\n")
        f.write(f"e: {e}\n")
        f.write(f"c: {c}\n\n")

Although he mixed some messages with Flag, we don’t know which one we want. But you can see that his public key index e is fixed at 3, so you can try using small public key index attack and explode every group! Next we look at the ciphertext encrypted-message.txt.

n: 12426348204210593270343924563278821305386892683425418957350363905840484905896816630189546938112358425679727243103082954824537007026886458498690134225705484501535835385800730412220192564706251228021192115494699150390312107794005569764411063907390563937247515046052549753641884721864426154021041082461015103337120756347692245843318676049947569653604616584167536958803278688355036036887022591104659059883622072052793378468850702811804337808760402077376453702190206077039468600466511349923882037572540505571672225260106649075841827340894515208811788428239691505001675042096850318994923571686175381862745049100863883977473
e: 3
c: 5065488652323342174251548936130018278628515304559137485528400780060697119682927936946069625772269234638180036633146283242714689277793018059046463458498115311853401434289264038408827377579534270489217094049453933816452196508276029690068611901872786195723358744119490651499187556193711866091991489262948739533990000464588752544599393

n: 19928073532667002674271126242460424264678302463110874370548818138542019092428748404842979311103440183470341730391245820461360581989271804887458051852613435204857098017249255006951581790650329570721461311276897625064269097611296994752278236116594018565111511706468113995740555227723579333780825133947488456834006391113674719045468317242000478209048237262125983164844808938206933531765230386987211125968246026721916610034981306385276396371953013685639581894384852327010462345466019070637326891690322855254242653309376909918630162231006323084408189767751387637751885504520154800908122596020421247199812233589471220112129
e: 3
c: 86893891006724995283854813014390877172735163869036169496565461737741926829273252426484138905500712279566881578262823696620415864916590651557711035982810690227377784525466265776922625254135896966472905776613722370871107640819140591627040592402867504449339363559108090452141753194477174987394954897424151839006206598186417617292433784471465084923195909989

n: 13985338100073848499962346750699011512326742990711979583786294844886470425669389469764474043289963969088280475141324734604981276497038537100708836322845411656572006418427866013918729379798636491260028396348617844015862841979175195453570117422353716544166507768864242921758225721278003979256590348823935697123804897560450268775282548700587951487598672539626282196784513553910086002350034101793371250490240347953205377022300063974640289625028728548078378424148385027286992809999596692826238954331923568004396053037776447946561334562767800447991022277806874834150264326754308297071271019402461938938062378926442519736239
e: 3
c: 86893891006724995283854813014390877172735163869036169496565461737741926829273252426484138905500712279566881578262823696620415864916590651557711035982810690227377784525466265776922625254135896966472905776613722370871107640819140591627040592402867504449339363559108090452141753194477174987394954897424151839006206598186417617292433784471465084923195909989

n: 19594695114938628314229388830603768544844132388459850777761001630275366893884362012318651705573995962720323983057152055387059580452986042765567426880931775302981922724052340073927578619711314305880220746467095847890382386552455126586101506301413099830377279091457182155755872971840333906012240683526684419808580343325425793078160255607072901213979561554799496270708954359438916048029174155327818898336335540262711330304350220907460431976899556849537752397478305745520053275803008830388002531739866400985634978857874446527750647566158509254171939570515941307939440401043123899494711660946335200589223377770449028735883
e: 3
c: 5065488652323342174251548936130018278628515304559137485528400780060697119682927936946069625772269234638180036633146283242714689277793018059046463458498115311853401434289264038408827377579534270489217094049453933816452196508276029690068611901872786195723358744119490651499187556193711866091991489262948739533990000464588752544599393

n: 12091176521446155371204073404889525876314588332922377487429571547758084816238235861014745356614376156383931349803571788181930149440902327788407963355833344633600023056350033929156610144317430277928585033022575359124565125831690297194603671159111264262415101279175084559556136660680378784536991429981314493539364539693532779328875047664128106745970757842693549568630897393185902686036462324740537748985174226434204877493901859632719320905214814513984041502139355907636120026375145132423688329342458126031078786420472123904754125728860419063694343614392723677636114665080333174626159191829467627600232520864728015961207
e: 3
c: 301927034179130315172951479434750678833634853032331571873622664843345454556713005601858152523700291841415874274186191308636935232309742600657257783870282807784519336918511713958804608229440141151963841588389502276162366733982719267670094167338480873020791643860930493832853048467543729024717103511475500012196697609001154401

n: 19121666910896626046955740146145445167107966318588247850703213187413786998275793199086039214034176975548304646377239346659251146907978120368785564098586810434787236158559918254406674657325596697756783544837638305550511428490013226728316473496958326626971971356583273462837171624519736741863228128961806679762818157523548909347743452236866043900099524145710863666750741485246383193807923839936945961137020344124667295617255208668901346925121844295216273758788088883216826744526129511322932544118330627352733356335573936803659208844366689011709371897472708945066317041109550737511825722041213430818433084278617562166603
e: 3
c: 38999477927573480744724357594313956376612559501982863881503907194813646795174312444340693051072410232762895994061399222849450325021561935979706475527169503326744567478138877010606365500800690273

n: 13418736740762596973104019538568029846047274590543735090579226390035444037972048475994990493901009703925021840496230977791241064367082248745077884860140229573097744846674464511874248586781278724368902508880232550363196125332007334060198960815141256160428342285352881398476991478501510315021684774636980366078533981139486237599681094475934234215605394201283718335229148367719703118256598858595776777681347337593280391052515991784851827621657319164805164988688658013761897959597961647960373018373955633439309271548748272976729429847477342667875183958981069315601906664672096776841682438185369260273501519542893405128843
e: 3
c: 38999477927573480744724357594313956376612559501982863881503907194813646795174312444340693051072410232762895994061399222849450325021561935979706475527169503326744567478138877010606365500800690273

n: 11464859840071386874187998795181332312728074122716799062981080421188915868236220735190397594058648588181928124991332518259177909372407829352545954794824083851124711687829216475448282589408362385114764290346196664002188337713751542277587753067638161636766297892811393667196988094100002752743054021009539962054210885806506140497869746682404059274443570436700825435628817817426475943873865847012459799284263343211713809567841907491474908123827229392305117614651611218712810815944801398564599148842933378612548977451706147596637225675719651726550873391280782279097513569748332831819616926344025355682272270297510077861213
e: 3
c: 38999477927573480744724357594313956376612559501982863881503907194813646795174312444340693051072410232762895994061399222849450325021561935979706475527169503326744567478138877010606365500800690273

n: 21079224330416020275858215994125438409920350750828528428653429418050688406373438072692061033602698683604056177670991486330201941071320198633550189417515090152728909334196025991131427459901311579710493651699048138078456234816053539436726503461851093677741327645208285078711019158565296646858341000160387962592778531522953839934806024839570625179579537606629110275080930433458691144426869886809362780063401674963129711723354189327628731665487157177939180982782708601880309816267314061257447780050575935843160596133370063252618488779123249496279022306973156821343257109347328064771311662968182821013519854248157720756807
e: 3
c: 301927034179130315172951479434750678833634853032331571873622664843345454556713005601858152523700291841415874274186191308636935232309742600657257783870282807784519336918511713958804608229440141151963841588389502276162366733982719267670094167338480873020791643860930493832853048467543729024717103511475500012196697609001154401

n: 22748076750931308662769068253035543469890821090685595609386711982925559973042348231161108618506912807763679729371432513862439311860465982816329852242689917043600909866228033526990181831690460395726449921264612636634984917361596257010708960150801970337017805161196692131098507198455206977607347463663083559561805065823088182032466514286002822511854823747204286303638719961067031142962653536148315879123067183501832837303731109779836127520626791254669462630052241934836308543513534520718206756591694480011760892620054163997231711364648699030108110266218981661196887739673466188945869132403569916138510676165684240183111
e: 3
c: 5065488652323342174251548936130018278628515304559137485528400780060697119682927936946069625772269234638180036633146283242714689277793018059046463458498115311853401434289264038408827377579534270489217094049453933816452196508276029690068611901872786195723358744119490651499187556193711866091991489262948739533990000464588752544599393

n: 15211900116336803732344592760922834443004765970450412208051966274826597749339532765578227573197330047059803101270880541680131550958687802954888961705393956657868884907645785512376642155308131397402701603803647441382916842882492267325851662873923175266777876985133649576647380094088801184772276271073029416994360658165050186847216039014659638983362906789271549086709185037174653379771757424215077386429302561993072709052028024252377809234900540361220738390360903961813364846209443618751828783578017709045913739617558501570814103979018207946181754875575107735276643521299439085628980402142940293152962612204167653199743
e: 3
c: 301927034179130315172951479434750678833634853032331571873622664843345454556713005601858152523700291841415874274186191308636935232309742600657257783870282807784519336918511713958804608229440141151963841588389502276162366733982719267670094167338480873020791643860930493832853048467543729024717103511475500012196697609001154401

n: 21920948973299458738045404295160882862610665825700737053514340871547874723791019039542757481917797517039141169591479170760066013081713286922088845787806782581624491712703646267369882590955000373469325726427872935253365913397944180186654880845126957303205539301069768887632145154046359203259250404468218889221182463744409114758635646234714383982460599605335789047488578641238793390948534816976338377433533003184622991479234157434691635609833437336353417201442828968447500119160169653140572098207587349003837774078136718264889636544528530809416097955593693611757015411563969513158773239516267786736491123281163075118193
e: 3
c: 86893891006724995283854813014390877172735163869036169496565461737741926829273252426484138905500712279566881578262823696620415864916590651557711035982810690227377784525466265776922625254135896966472905776613722370871107640819140591627040592402867504449339363559108090452141753194477174987394954897424151839006206598186417617292433784471465084923195909989

good! Now that you have discovered its weakness by looking at the encryption script, let’s go straight to writing the Exploit.

import gmpy2
from Crypto.Util.number import long_to_bytes


def decrypt(cipher: dict) -> str:
    e = cipher["e"]
    n = cipher["n"]
    c = cipher["c"]
    k = 0
    while True:
        m, is_root = gmpy2.iroot(k * n + c, e)
        if is_root:
            break
        else:
            k += 1
    return long_to_bytes(m).decode()


with open(r"encrypted-messages.txt", "r") as f:
    file = f.read()

file = file.split("\n\n")
file.pop()

ciphers = []
for c in file:
    cipher = {}
    c = c.split("\n")
    for item in c:
        key, value = item.split(": ")
        cipher[key] = int(value)
    ciphers.append(cipher)

plaintext = ""
for cipher in ciphers:
    plaintext += decrypt(cipher) + "\n"

print(plaintext)

Voila! Flag 就出來啦~

picoCTF{1_gu3ss_p30pl3_p4d_m3ss4g3s_f0r_4_r34s0n}

substitution0

This question gives an encrypted ciphertext, as follows.

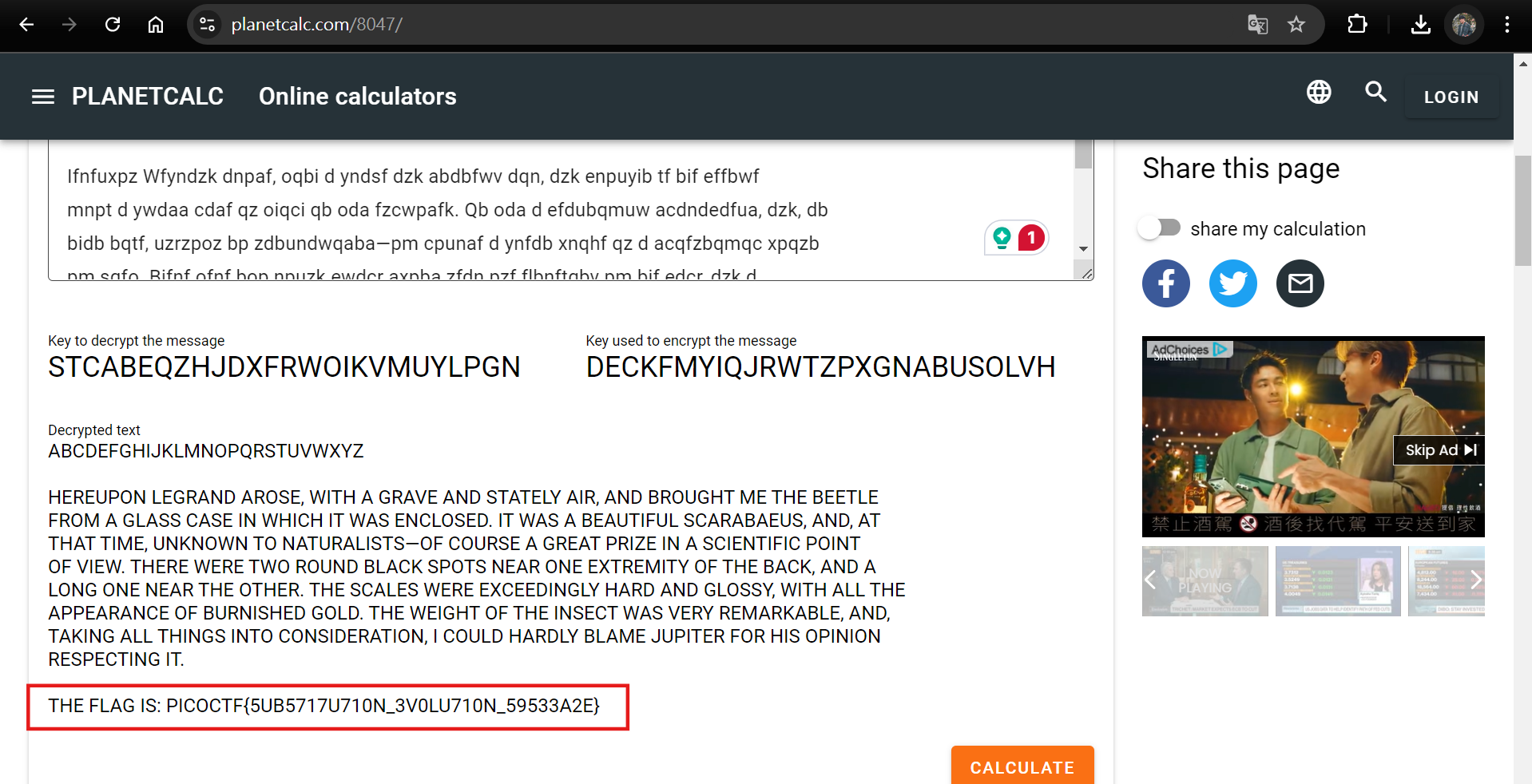
DECKFMYIQJRWTZPXGNABUSOLVH

Ifnfuxpz Wfyndzk dnpaf, oqbi d yndsf dzk abdbfwv dqn, dzk enpuyib tf bif effbwf
mnpt d ywdaa cdaf qz oiqci qb oda fzcwpafk. Qb oda d efdubqmuw acdndedfua, dzk, db
bidb bqtf, uzrzpoz bp zdbundwqaba—pm cpunaf d ynfdb xnqhf qz d acqfzbqmqc xpqzb
pm sqfo. Bifnf ofnf bop npuzk ewdcr axpba zfdn pzf flbnftqbv pm bif edcr, dzk d
wpzy pzf zfdn bif pbifn. Bif acdwfa ofnf flcffkqzywv idnk dzk ywpaav, oqbi dww bif
dxxfdndzcf pm eunzqaifk ypwk. Bif ofqyib pm bif qzafcb oda sfnv nftdnrdewf, dzk,
bdrqzy dww biqzya qzbp cpzaqkfndbqpz, Q cpuwk idnkwv ewdtf Juxqbfn mpn iqa pxqzqpz
nfaxfcbqzy qb.

Bif mwdy qa: xqcpCBM{5UE5717U710Z_3S0WU710Z_59533D2F}

The last line looks a lot like Flag, but because it gives a large paragraph of text, you can directly use brute force to crack it. I recommend using this website, just enter the entire paragraph and it will help you find the most likely solution.

picoCTF{5UB5717U710N_3V0LU710N_59533A2E}

substitution1

Logically speaking, this question should be the same as the previous question, but I think he may have changed the question and then forgot to change the answer, because I have seen many people’s writeups with the same answer, but the Flag of each Personal is different XD, so I just Skip it first.

#substitution2

Use the same online tool for this question as well.

picoCTF{N6R4M_4N41Y515_15_73D10U5_42EA1770}

#ReadMyCert

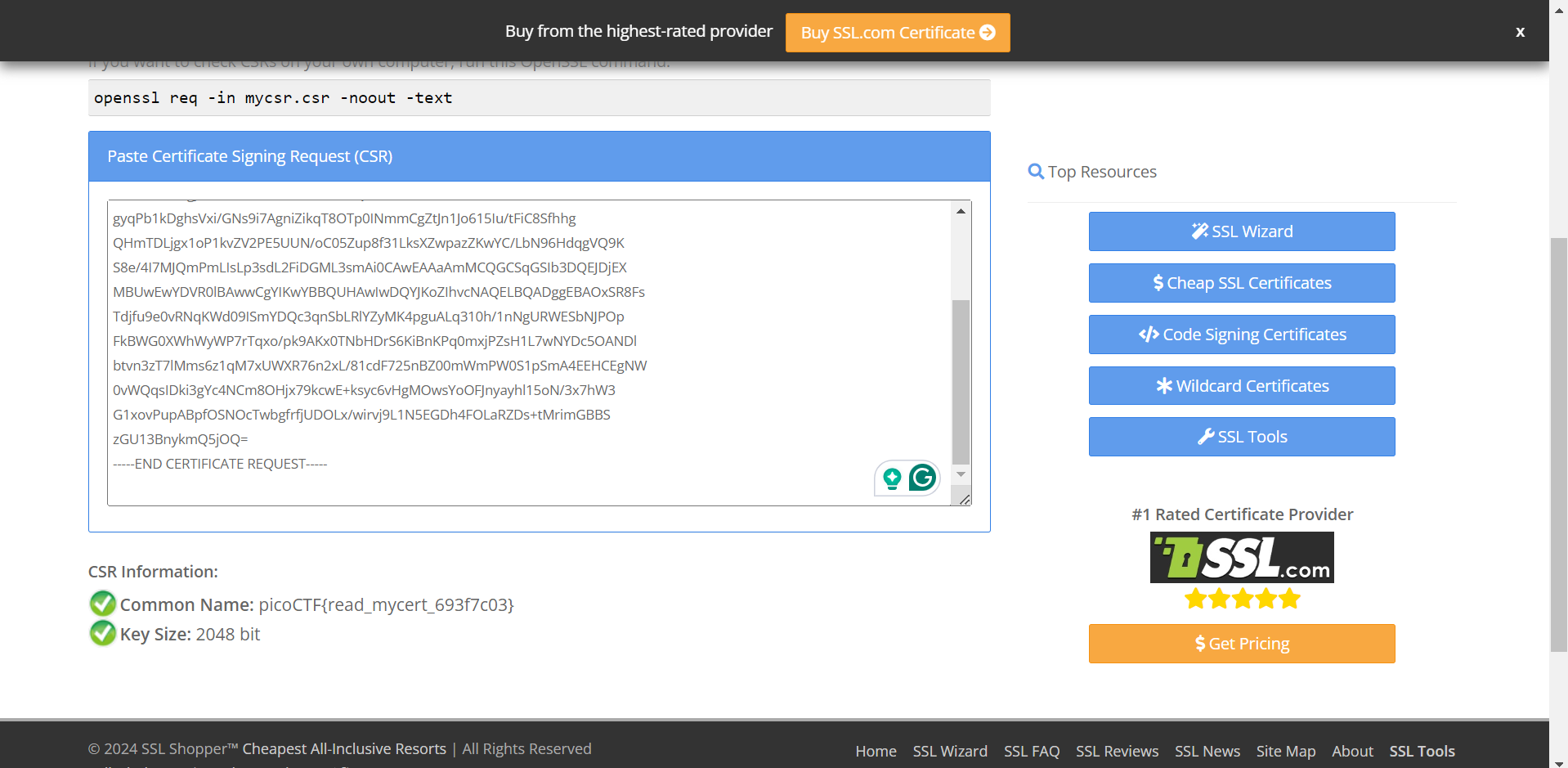
This question gives a CSR (Certificate Signing Request) file and requires us to check this file. Because the encoding method of the CSR file is a specific format, not simply Base64 encoding, we can use the following command to view it.

openssl req -in <yourcsr.csr> -noout -text

But for convenience, we can directly use online CSR Decoder to help us decode.

picoCTF{read_mycert_693f7c03}

#transposition-trial

Let’s look at the title description first.

Our data got corrupted on the way here. Fortunately, nothing got replaced, but every block of 3 got scrambled around! The first word seems to be three letters long, maybe you can use that to recover the rest of the message.

This represents blocks of three words, and each block is scrambled in the same way. The ciphertext looks like this.

heTfl g as iicpCTo{7F4NRP051N5_16_35P3X51N3_V091B0AE}2

We can find that the first three words are The, so we can infer that the way he scrambles it is that the last one in each Block becomes the first, and the rest remain unchanged. Then let’s construct an Exploit.

cipher = "heTfl g as iicpCTo{7F4NRP051N5_16_35P3X51N3_V091B0AE}2"

flag = ""
for i in range(0, len(cipher), 3):
    block = cipher[i : i + 3]
    flag += block[-1] + block[0:-1]

print(flag)

That’s it!

picoCTF{7R4N5P051N6_15_3XP3N51V3_109AB02E}

spelling-quiz

This question gives three files, encrypt.py, flag.txt and study-guide.txt. Let’s take a look at the encryption script first.

import random
import os

files = [
    os.path.join(path, file)
    for path, dirs, files in os.walk(".")
    for file in files
    if file.split(".")[-1] == "txt"
]

alphabet = list("abcdefghijklmnopqrstuvwxyz")
random.shuffle(shuffled := alphabet[:])
dictionary = dict(zip(alphabet, shuffled))

for filename in files:
    text = open(filename, "r").read()
    encrypted = "".join([dictionary[c] if c in dictionary else c for c in text])
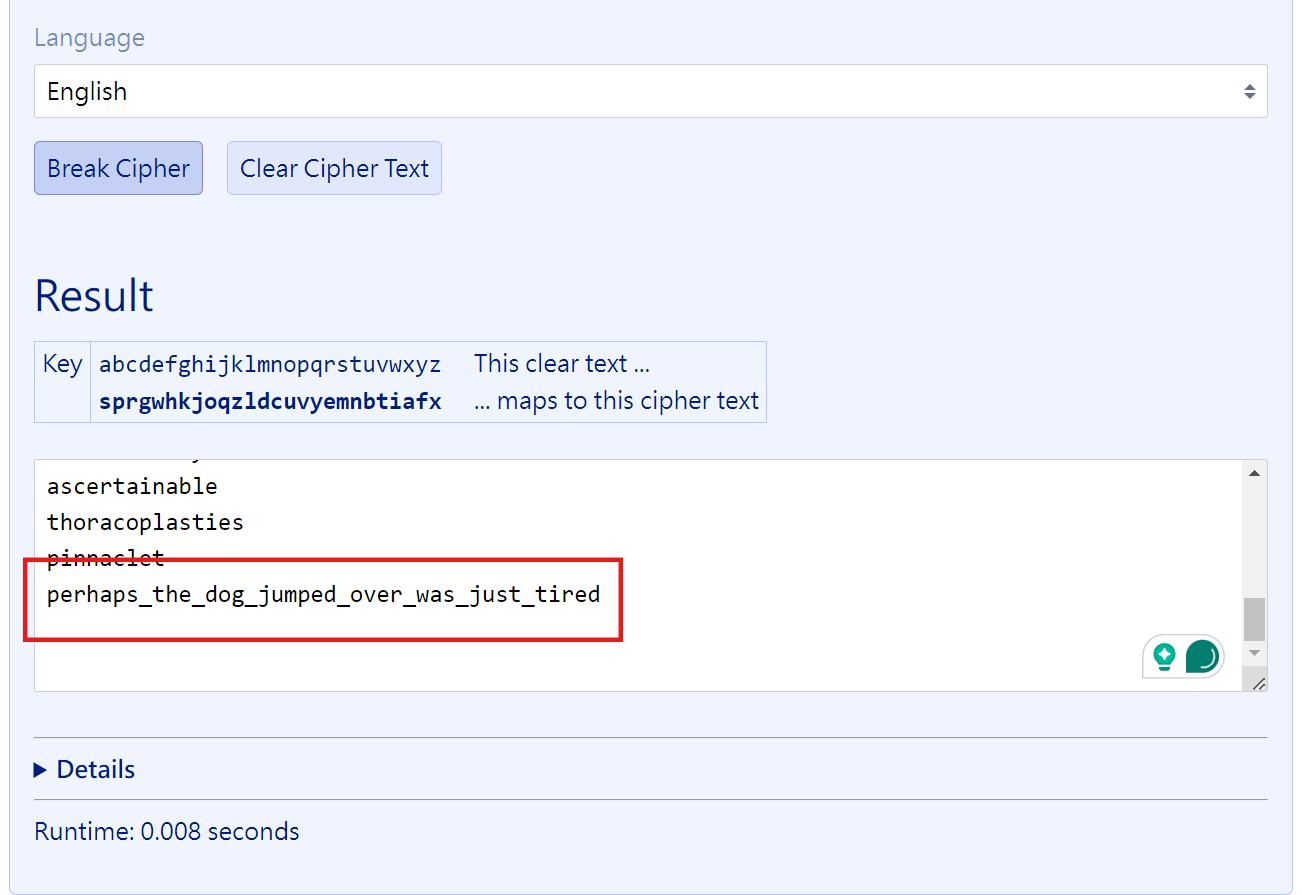
    open(filename, "w").write(encrypted)

It can be seen that he is a Substitution Cipher. Then because we are sure that study-guide.txt contains normal words (as the question says), we can directly connect flag.txt to the back of study-guide.txt, and then use it to give some lines Just use the tool to decrypt it (Frequency Attack). Here I use this tool.

Finally, remember to wrap it with picoCTF{}.

picoCTF{perhaps_the_dog_jumped_over_was_just_tired}

rail-fence

This question gives a secret text, as follows.

Ta _7N6D8Dhlg:W3D_H3C31N__387ef sHR053F38N43DFD i33___N6

It is a classic fence cipher. You can directly use the online tool to decrypt it. Remember to turn on the following option. Then you can solve Flag.

picoCTF{WH3R3_D035_7H3_F3NC3_8361N_4ND_3ND_83F6D8D7}

Dachshund Attacks

TODO: Wiener’s attack

from Crypto.Util.number import *
from pwn import *
import gmpy2


def continued_fraction(n, d):
    """Returns the continued fraction representation of a rational number n/d"""
    cf = []
    while d != 0:
        cf.append(n // d)
        n, d = d, n % d
    return cf


def convergents(cf):
    """Returns the convergents from a continued fraction"""
    n0, d0 = 0, 1
    n1, d1 = 1, 0
    convergents = []

    for q in cf:
        n2 = q * n1 + n0
        d2 = q * d1 + d0
        convergents.append((n2, d2))
        n0, d0 = n1, d1
        n1, d1 = n2, d2

    return convergents


def wiener_attack(e, n):
    """Performs Wiener's attack using gmpy2 to recover d"""
    cf = continued_fraction(e, n)
    convs = convergents(cf)

    for k, d in convs:
        if k == 0:
            continue
        # Calculate phi using the convergent d
        if (e * d - 1) % k == 0:
            phi = (e * d - 1) // k
            # Calculate the discriminant of the quadratic equation
            b = n - phi + 1
            discriminant = b**2 - 4 * n
            if discriminant >= 0:
                sqrt_disc = gmpy2.isqrt(discriminant)
                if sqrt_disc * sqrt_disc == discriminant:
                    print(f"Private key found: d = {d}")
                    return d
    return None


r = remote("mercury.picoctf.net", 37455)
r.recvuntil(b"e: ")
e = int(r.recvline().strip())
r.recvuntil(b"n: ")
n = int(r.recvline().strip())
r.recvuntil(b"c: ")
c = int(r.recvline().strip())


d = wiener_attack(e, n)
m = pow(c, d, n)
print(long_to_bytes(m))

waves over lambda

After this question is connected, it will spit out cipher text, and then a Substitution cipher. Take it directly to [Online Word Frequency Analysis] (https://www.guballa.de/substitution-solver) to crack it.

frequency_is_c_over_lambda_agflcgtyue

Then this question is not wrapped with picoCTF{}.